WisFaq!

Minimale oppervlakte prisma

Ik zou graag antwoord willen op deze vraag, want ik kom er niet uit.

Gegeven: een driezijdig prisma en een driezijdige piramide elk met een vaste inhoud van 1000 dm³ en een grondvlak in de vorm van een gelijkzijdige driehoek.

Zoek uit bij welke afmetingen de oppervlakte zo klein mogelijk is.

michelle
20-2-2002

Antwoord

Deze vraag is al een keer beantwoord voor een cilinder (zie onder). Het principe gaat hier natuurlijk ook op.

PRISMA
inh=G·h
Omdat je de inhoud kent:
1000=G·h
h=1000/G

Noem een ribbe van het grondvlak r. Dan is G=¹/₄·r²·3

Ik ga nu de oppervlakte uitdrukken in 'r':
O(r)=2·G + 3·r·h=2·¹/₄·r²·3 + 3·r·1000/(¹/₄·r²·3)
O(r)=¹/₂·r²·3 + (40003)/r

Deze 'functie' moeten we minimaliseren.
Dus eerst maar eens de afgeleide:
O'(r)=3·r - (40003)/r²
O'(r)=0 voor r=10·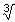4

Voor r=10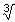4 hebben de kleinste oppervlakte (Nog wel even controleren met een tekenverloop of het inderdaad een minimum is en bereken zelf h).

DRIEZIJDIGE PIRAMIDE
inh=1/3·G·h
We kennen de inhoud:
1000=1/3·G·h
h=3000/G

Noem de ribbe van het grondvlak r. Dan is G=¹/₄·r²·3
Verzin nu zelf een formule voor de oppervlakte en probeer het nu zelf!

Zie Cilinder [http://www.wisfaq.nl/showrecord3.asp?id=170]

WvR
20-2-2002