Bij de volgende antwoorden staan in totaal 3 algoritmen beschreven:
Rekenkundig bewijs voor de methode van Van der Blij
Hoe maak je een even tovervierkant?
In de eerste link staat ook een bewijs van het algoritme.
In de tweede link staan twee algoritmes voor magische vierkanten van even orde.
De diagonale methode
Om erachter te komen waarom een algoritme werkt is het goed om eens een voorbeeld te maken.
Zo heb ik hieronder een vierkant van orde 8 gemaakt.
Je begint de getallen in het vierkant te zetten
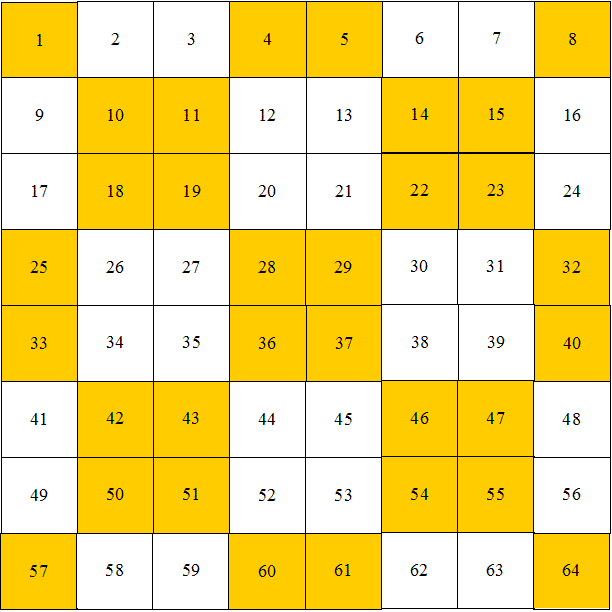
en dan ga je de getallen verwisselen.
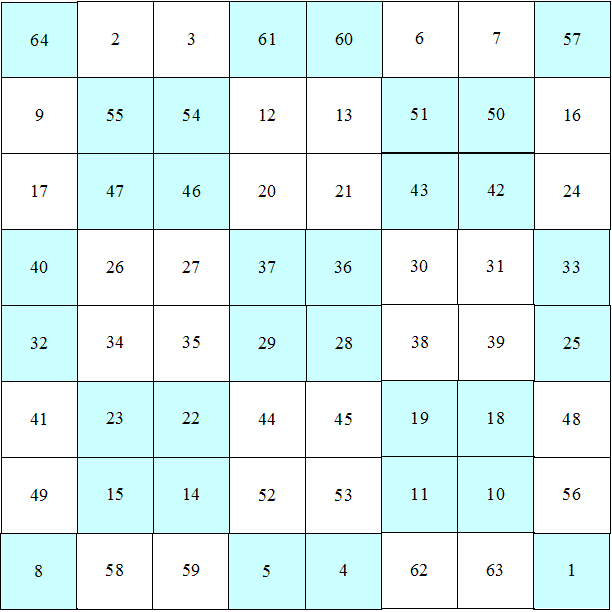
We kijken hier naar het geval je de getallen op de diagonalen verplaatst.
De getallen op de grote diagonalen blijven na het verwisselen ook op de diagonalen staan. Je kunt dus al beginnen met te bewijzen dat de som van deze getallen klopt. Kijk dan eens naar de sommen van de getallen in de rijen en de kolommen voordat je ze hebt verwisseld.
Wat valt je op?
Misschien kun je nu zelf wel beredeneren waarom deze methode werkt.
De tweede methode van Strachey kun je nu misschien zelf proberen te beredeneren.
gm
5-11-2003