WisFaq!

Draak

Hoi,
Ik heb een meningsverschil met mijn leraar en ik zou graag bewijzen dat ik juist ben, maar mijn berekeningen kloppen niet. Kunnen jullie mij helpen? Dit is de vraag: er zijn 65536 lijnstukjes in de figuur en in de eerste stap waren het er 2, nu moest ik bewijzen in hoeveel stappen ik de figuur krijg (dit is niet de vraag want die heb ik al opgelost het waren 16 stappen), maar nu moet ik zien hoe lang de curve in stap 16 is? (de beginsituatie (stap 1 dus)is de lengte 1) en er stond ook bij dat ik de stelling van Pythagoras moest gebruiken maar het lukt niet. Kunnen jullie mij helpen?
Alvast bedankt

Mike
13-10-2003

Antwoord

Lekker verwarrend... Je schrijft 'in' de eerste stap... ik zou zeggen na de eerste stap. De beginsituatie is dus een enkel lijntje van lengte 1. Bij de draakkromme wordt een lijntje met lengte m vervangen door twee lijnstukjes met elk een lengte van m/Ö2, dus in totaal steeds mÖ2 keer zo groot...
In onderstaande figuur (na stap 1) kan je dat laten zien met de stelling van Pythagoras:



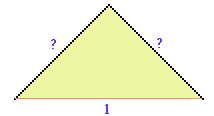
Ga maar na! ?²+?²=1²

We krijgen dan:



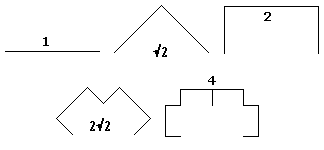
De totale lengte:
Het begin: 1
Na 1 stap: Ö2
Na 2 stappen: 2
Na 3 stappen: 2Ö2
...
Na n stappen: (Ö2)ⁿ

Na 16 stappen heb je dus een totale lengte van (Ö2)¹⁶=256

Zie Meer over de draakkromme [/zoeken.asp?search=draak&vraagaan=FALSE&exact=and&categorie= ]

WvR
13-10-2003