WisFaq!

Inhoud berekenen omwentelingslichaam met GR: Ti 82

Okeej, zoals jij ook vast wel weet, kun je de inhoud van een omwentelingslichaam L berekenen op een algebraische manier door te integreren, primitiveren etc. Maar de volgende vraag moet gedaan worden met een Ti 82, echter als je niet eens kunt helpen zou je me toch op weg kunnen helpen denk ik,

Okeej, hier is mijn vraag dan.......
Gegeven zijn de functies f(x)=ln(x-1) en g(x)=2-lnx V is het vlakdeel dat wordt ingesloten door de grafiek van f, de x-as, de y-as en de lijn y=2. W is het vlakdeel dat wordt ingesloten door de grafieken van f en g en de x-as.
c) bereken de inhoud van het omwentelingslichaam dat ontstaat als W om de y-as wentelt.

Ik weet dat je niet simpelweg bij het berekenen 2 en het snijpunt van g met de x-as kan nemen (b, welke na berekening e² blijkt te zijn), maar hoe moet het dan wel. De uitwerkingen die ik heb gelezen, en waarna ik het nog steeds niet snap geven het volgende:

y= ln(x-1) geeft x=e -tot de yde- +1 , dit snap ik nog wel.
Vervolgens zeggen ze aangezien y=2-lnx, geldt x=e -tot de 2-y-. Dit snap ik niet, ik zou graag willen weten met welke stappen je hier x in y uitdrukt. Hierna moet je volgens de uitwerkingen invoeren y₁=$\pi$(e tot de xde +1)² en y₂=$\pi$(e tot de 2-x)². Met de GR kun je vervolgens met een bepaalde optie de hoogte van de n cilindertjes uitrekenen en als het ware dx. in de integraal-formule wegwerken. Met deze formules zou je dus de inhoud van het betreffende omwentelingslichaam moeten kunnen uitrekenen. Dit doen ze als volgt: I= $\int{}$ (met grenzen a=0 en b= 0.817) (y₂-y₁)dx hetgeen het antwoord 52.04 zou moeten opleveren. Ik snap ook niet hoe dit de I van van het omwentelingslichaam -wat ontstaat als je W laat wentelen om de y-as- voor kan stellen. Hopelijk krijg ik binnekort antwoord, ik moet namelijk nog veel doen voor de test op maandag.

Alvast bedankt dan he , Dione

Dione Nozza
11-10-2003

Antwoord

Volgens mij valt deze vraag uiteen in een paar onderdelen.

1.
Omdat je wentelt om de y-as kan het handig zijn om de functies 'om te draaien'. Dat wil zeggen dat je x schrijft als functie van y.

y=ln(x-1) wordt dan:
e^y=x-1
x=e^y+1
Dus: y=e^x+1

y=2-lnx wordt dan:
e^y=e^2-ln(x)
e^y=e²:e^ln(x)
e^y=e²:x
x=e²:e^y
x=e^2-y
Dus: y=e^2-x

2.
Eerst maar eens een tekening van de nieuwe situatie:



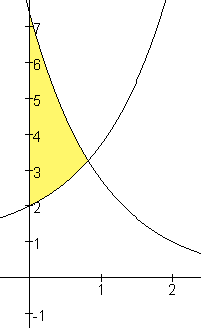
Nu gaan we het gele vlak wentelen om de x-as. We kunnen dan nu de integralen gebruiken zoals je die ook op de formulekaart kan vinden (zie links bij formules).

Inhoud van het omwentelingslichaam dat ontstaat door de grafiek van de functie f op het interval [a, b] om de x-as te wentelen:



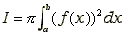
Eerst maar eens het snijpunt berekenen:
e^x+1=e^2-x
x0,8171 (met je GR en intersect)

Het gaat dus om:



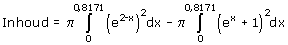
Dit kunnen we benaderen met de GR met de functie fnInt:
Met:

Y1=e^(x)+1
Y2=e^(2-x)

..dan kan je met:
fnInt(p*Y2²,X,0,0.8171)-fnInt(p*Y1²,X,0,0.8171)52,04
de gevraagde inhoud berekenen.

Zie ook: Oppervlakte berekenen en inhoud berekenen

WvR
11-10-2003