WisFaq!

Discrete kansmodellen

Ik had wat vraagjes die ik niet snap en ik heb overmorgen toets hierover! Probleem dus!

Mijn vragen zijn:

2 tennissers spelen finale, winnaar is de gene die het eerst 3 sets op zijn naam heeft. stochast T is het aantal te spelen sets.
a) stel kansverdeling voor T op
b) bereken E(t)

uit een pak speelkaarten met 52 kaarten trek je een kaart, als het een aas is win je 10 euro, als het een heer, boer of vrouw is win je 5 euro en voor elke andere kaart moet je 2 euro betalen. Wat is de winstverwachting?

Het antwoord op deze vraag is een verlies van 8 cent maar ik heb geen idee hoe ze hier aan komen.

In een bak bevinden zich 2 witte en 3 zwarte balletjes. Frank, miriam, ralf, willy nemen in deze volgorde ieder een balletje uit de bak zonder dat ze het terugleggen. De eerste die een wit balletje trekt krijgt 10 euro. Bepaal voor de vier het te verwachte bedrag

Antwoord hierop is, frank 4, miriam 3 ralf 2 en willy 1

van een binomiaal verdeelde stochast X weet je dat de verwachtingswaarde 2[2/3] is en de standaardafwijking is 1¹/₃. Bereken P(X=4)

Antwoord hier op is 0.1708

Ik hoop dat iemand me kan helpen want ik kom er niet uit!
Alvast bedankt.

Laura
4-10-2003

Antwoord

1.
Bij de tenniswedstrijd staat niet dat de spelers even sterk zijn... dat zou wel handig zijn om te weten. Zou het uitmaken denk je? Misschien moet je er maar van uit gaan dat de kans om een set te winnen een half is.
Teken eens een kansboom!



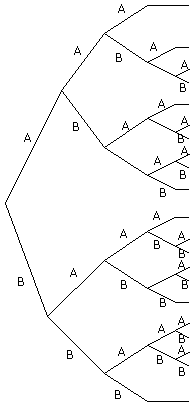
Schrijf bij alle mogelijke uitkomsten de kans op die gebeurtenis. Tel de kansen op 3 sets op, tel de kansen op 4 sets op en tel de kansen op 5 sets op. Dit geeft een kansverdeling op 3, 4 of 5 sets. Samen zijn ze natuurlijk 1.

De verwachtingswaarde is dan:
P(3 sets)·3 + P(4 sets)·4 + P(5 sets)·5

2.
Bereken P(aas), P(heer, vrouw of boer) en P(geen aas, geen heer, geen vrouw, geen boer). De winstverwachting kan je dan berekenen met:
P(aas)·10 + P(heer, vrouw of boer)·5 + P(geen aas, geen heer, geen vrouw, geen boer)·-2
Ik kom dan echter niet uit op 8 eurocent...

3.
E(Frank)=P(wit)·10=²/₅·10=4
E(Mirjam)=P(wit)·10=³/₅·²/₄·10=3
E(Ralf)=P(wit)·10=³/₅·²/₄²/₃·10=2
Enz...

4.
Er geldt:
m=n·p=2²/₃ (1)
s=Ö(n·p·(1-p))=1¹/₃ (2)
Uit (1) kan je halen n=⁸/_3p
Vul dit in in (2) en je weet p en n (nou ja even oplossen natuurlijk...:-).
Daarmee kan je P(X=4) berekenen:
Daarna nog vragen? Dan horen we het wel...

WvR
5-10-2003