WisFaq!

Evenwijdige lijnen snijden in het oneindige?

Ik heb me laten vertellen dat evenwijdige rechten elkaar in het oneindige snijden. Dat wil ik best aannemen, maar kan je dat ook (op een begrijpelijke manier) bewijzen?

Bram Goetschalckx
10-2-2002

Antwoord

De definitie van evenwijdigheid is nu juist dat de lijnen elkaar NIET snijden. Zeggen dat twee evenwijdige lijnen elkaar snijden in het oneindige is dus zeggen dat ze elkaar NIET snijden!

Als je een perspectief-tekening maakt, dan blijkt dat evenwijdige lijnen door één punt gaan. Misschien dat daar deze 'gedachte' zijn oorsprong vindt?

In Lessen in Projectieve Meetkunde van Martin Kindt (een aanrader!) staat bij onderstaand plaatje het bewijs:



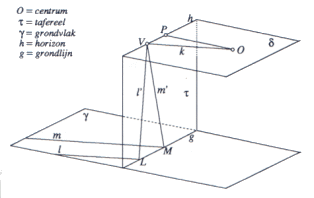
Ik ga het bewijs hier niet opschrijven, maar misschien kun je, kijkend naar de tekening, zelf al een beetje bedenken hoe het zit (let vooral op grondvlak, tafereel, O(og?) en zo...).

l en m zijn evenwijdige lijnen in het grondvlak. In het vlak t zie je l' en m' (dat is wat je ziet op de 'tekening') wel snijden. En waar snijden ze elkaar? Op de horizon! (als g loodrecht op t staat tenminste)

Het is nog veel erger! Als je de grafiek van y=x² tekent in perspectief zie je een ellips! (zie de omslag van het genoemde boek!) Conclusie: de twee takken van een parabool snijden elkaar in het oneindige!?

WvR
10-2-2002