WisFaq!

Re: Grafieken op een weg met stelling van Pythagoras

Nee zo niet :-)

Je tekent het verder goed, maar als de afstand van de oorsprong naar punt A verandert, verandert ook de afstand van de oorsprong naar punt B. Als de auto dus in de oorsprong staat. is de afstand Ooorsprong-A √3²+1²
Druk nou de afstand Oorsprong-B uit in Oorsprong-A
Dus Oorsprong-B(=y)= ···lastige formule met als X,Oorsprong A···

Het is dus niet zo simpel als je denkt!

Mystic
26-9-2003

Antwoord

Hoi,

Bij nader inzien is je probleem het volgende. Je beweegt volgens de X-as in een punt p(t,0) voor t>=0. De afstand tot a(3,1) noem je x, de afstand tot b(5,-2) is y. Je wil de plot van (x,y) ifv t.

x=sqrt[(3-t)²+(1-0)²]=sqrt[t²-6t+10] (1)
y=sqrt[(5-t)²+(-2-0)²]=sqrt[t²-10t+29] (2)

Dit is een parametrische kromme. Je vindt een schetsje in volgend plaatje.



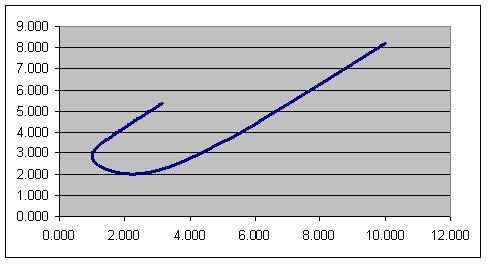
Zoals je ziet is het geen functie in functie van x, maar dit kon je intuïtief al verwachten: er is (soms) meer dan 1 positie op de X-as waar je op een bepaalde afstand y van b staat en dan sta je ook op verschillende afstanden x van a (namelijk waar d(p,b)<=d(b,0) - aan jou om die t-conditie op te stellen)... In het beste geval kan je een impliciete vergelijking in x en y of 2 expliciete functies van y naar x opstellen, maar dit is volgens mij een puur academische oefening...

Je vindt de split door dx/dt=0 op te lossen, dit geeft je de t voor de linkergrens. Fysisch kan je het ook inzien: je komt dichtst bij a wanneer je je in de projectie op de weg bevindt, dus voor t=3. De afstand is dan inderdaad 1. Praktisch zou je dus 2 functies kunnen expliciteren: één voor 0<=t<=3 en een andere voor t>3.

Concreet kan je (1) en (2) kwadrateren en van elkaar aftrekken. Zo vallen die termen in t² weg en kan je t als functie van x en y schrijven. Dit plug je dan in (1) of (2) en je kwadrateert de vierkantswortels weg. Dan hebben we al een impliciete 4de graadsvergelijking in x en y (eigenlijk in x² en y²). Bekijk dit als vierkantsvergelijking in y² en je kan dan 2 functies opstellen die y² en dus y uitdrukken in functie van x. Het leuke rekenwerk laat ik aan jou...

Strikt genoemen liet jij t enkel tot 5 lopen. Dit is het punt waar de curve dichtst tegen de X-as loopt. Eigenlijk kan je beter x naar y expliciteren. Dit kan je dan in 1 functie schrijven. De berekening is hetzelfde, behalve dat je een vierkantsvergelijking in x² oplost en t<=5 veronderstelt.

Groetjes,
Johan

andros
26-9-2003