WisFaq!

Re: Inverse formule (affine cipher) y=ax+b(mod26)

bedankt voor de snelle reactie! maar ik begrijp niet hoe je op die sets komt. waarom hoort 9 bij 3? en 21 bij 5? enz? hoe kan je dat berekenen?

neeltje
19-9-2003

Antwoord

Hoi,

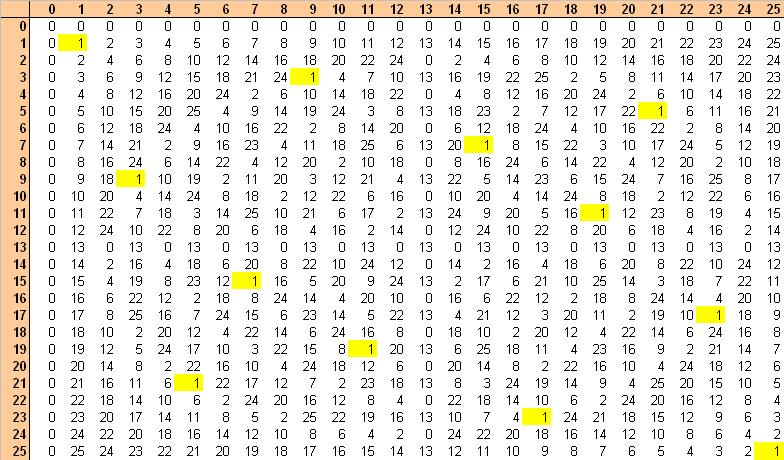
9 en 3 zijn elkaars inverse modulo 26: 9.3=27=1. Hetzelfde voor de andere setjes van 1 of 2 elementen. Ik heb die gevonden door een product-tabel te maken (in Excel): horizontaal 0..25 en vertikaal 0..25. In elke cel zet ik het product modulo 26. Overal waar een 1 als product komt, heb je inversen. Omdat . mod(26) commutatief is, is de tabel symmetrisch.
Voor grotere modulo's is het niet te doen om die tabel op te stellen. Daar moet je de Diophantische vergelijking ax+my=1 oplossen naar x. Hiervoor bestaan een aantal gespecialiseerde technieken.



Je kan ook volgende link gebruiken op WisWijzer (met dank aan Willem voor de hint)..

Groetjes,
Johan

andros
19-9-2003