WisFaq!

Rechthoekige driehoeken

Ik heb een probleem met een oefening over goniometrie. Ik zal proberen om de oefening zelf te maken, maar kunnen jullie mij de eerste stap geven?

Opg: In een rechthoekige driehoek abc zijn B' en C' de projecties van de rechthoekszijden B en C op de schuine zijde. H is de hoogte op de schuine zijde. Bereken cos c in twee rechthoekige driehoeken en leid eruit af dat:
B²= A.B'
Bereken daarna tg b en cotg c en leid eruit af dat:
H²=B.C

Ik denk dat je de formules van de rechthoekige driehoek moet gebruiken, maar ik weet niet welke.

Ik heb ook nog een tweede opgave, maar die is niet zo dringend.

opg: In de driehoek abc laat men uit b de loodlijn neer op ac. Deze loodlijn vormt een hoek van 45° met ba en van 60° met bc. Bewijs nu dat:
2B= A³Ö + 2Ö2

Verhoeven Jürgen
8-9-2003

Antwoord

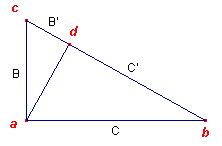
Zie ook het plaatje hierboven.
In driehoek abc is cos(c) = B/A (aanliggende rechthoekszijde gedeeld door de schuine zijde)
In driehoek acd is cos(c) = B'/B
En de volgende stap moet je zelf maar zetten (daar vraag je trouwens om).

Je schrijft H² = B.C, maar je bedoelt waarschijnlijk H² = B'.C'
In driehoek abd: tan(b) = H/C'
In driehoek acd: cotg(c) = ...
Kijk ook eens naar driehoek abc:
tan(b) = B/C
en in die zelfde driehoek abc: cotg(c) = ...
En de rest laat ik weer aan jou!


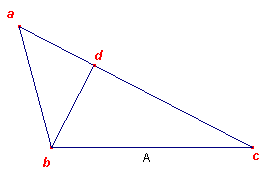
En de tweede vraag. Voor de oplossing daarvan geef ik een aantal stappen (zie ook weer het plaatje).
- Bereken eerst de andere hoeken in de driehoeken bcd en abd.
- Wat weet je nu al van [bd] en [ad]?
In driehoek bcd is sin(c) = [bd]/[bc] = [bd]/A
- Weet je de werkelijke waarde van sin(c)? Je kent immers de grootte van hoek c.
- Je kan dan aantonen, dat [bd] = ¹/₂A
- Bereken nu (wellicht met gebruik van sin(60) = ¹/₂Ö3) hoe groot [cd] is.
- En [ad] is nu ook bekend.
Als je alles goed gedaan hebt, moet je nu vinden:
2B = A(1 + Ö3)
En dus niet het antwoord, dat in je vraag staat.

Ik hoop dat je er zo uitkomt. Ik verwacht eigenlijk van wel...

dk
8-9-2003