WisFaq!

Relatie tussen een deling en exponentie

hoi,

ik kwam achter een psuedo-wiskunde formule (mijn wiskunde termen zijn niet echt al te best :)) dat er een relatie zit tussen een deling en een exponentie..

x/y = x*( (10^(length y)) - y)^0 * 10^(-(length y)*1) +
x*( (10^(length y)) - y)^1 * 10^(-(length y)*2) +
x*( (10^(length y)) - y)^(n-1) * 10^(-(length y)*n) + ...

waarbij ^ 'tot de macht' betekend.. en
'length y' het aantal decimalen van y..

dus stel: x = 1 en y = 9
1/9 = 1*((10^1)-9)^0 * 10^(-1*1) +
1*((10^1)-9)^1 * 10^(-1*2) +
...
waar dus weer uit volgt:
1/9 = 0.1 + 0.01 + 0.001 + 0.0001 + ...

dit geldt ook bij bv de inverse 89..
1/89 = 1*10^-2 + 11*10^-4 + 121*10^-6 + 1331*10^-8 + ..

een simpel voorbeeld om het in 1 oog opslag te zien is
1/99999998 ...

wat nu het aparte is... elke breuk eindigt of is reperterend.. wat nogal raar is als je et bekijkt van
de exponentiele optelling.. een eindeloos proces maar door
het optellen komt er toch ritme in...

is hier een of andere theory over?.. of heb ik nou een
geweldige ontdekking gedaan? :)))

Tim Gerritsen
3-9-2003

Antwoord

Hoi,

mooi is dat hé dat dat je zo'n algoritme vindt en ziet dat het werkt. Je vraagt dus naar de theoretische onderbouwing.
Deze berust op de som van een oneindige meetkundige rij.
Ik zal dat hieronder aan de hand van het voorbeeld met 1/89 laten zien.
Als je niet weet hoe je de som van een meetkundige rij moet berekenen bestudeer dan eerst even de volgende link:
meetkundige rij
We nemen nu het voorbeeld van die 1/89:

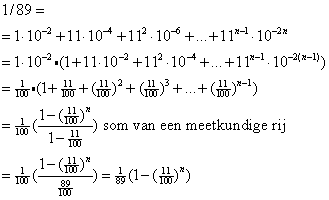
Omdat (11/100)ⁿ nadert tot 0 als n heel groot wordt (n nadert tot oneindig) komt er uiteindelijk 1/100*1/(89/100)=1/89 uit.

Het is aardig om eens te onderzoeken hoe efficient jouw algoritme is daarom even onderstaand scriptje:

teller
noemer
aantal stappen

(probeer eens 1/89, 1/11, 1/5).

In het voorbeeld met 1/89 gaat het vrij vlug omdat de reden van de meekundige rij 11/100=0,11 is en 0,11ⁿ vrij snel tot 0 nadert.
In het geval 1/11 is de reden 0,89. En 0,89ⁿ nadert niet bepaald snel tot 0.

hk
5-9-2003