WisFaq!

Verdeling van druppels in een neerslag

De verdeling van waterdruppels in een wolk worden beschreven met aantal en grootte. Deze beschrijving komt tot stand op besis van "geometrische standaarddeviatie (q) van een log-normale verdeling op massa basis".
Massa van een druppel is een functie van de straal (4/3r³).
Hiervoor geldt q = Ö(r_84.13%/r_15.87%).
Waar komen de getallen 84.13% en 15.87% vandaan?

hennie
22-8-2003

Antwoord

Kijk eerst even naar de standaardnormale verdeling:



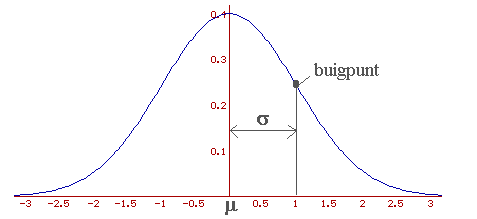
De standaard score z=1 (het buigpunt) betekent één keer de standaarddeviatie 'rechts' van het gemiddelde.
De oppervlakte links van z=1: F(1)=0,8413
Net zo geldt: F(-1)=0,1586

Neem aan dat je van een normale verdeling zou weten:
P(X14,5)=0,8413
P(X10,5)=0,1586
Wat is dat de standaarddeviatie?

Antwoord: s=(14,5-10,5)/2=2

Nu gaat het hier niet om de normale verdeling, maar om de log-normale verdeling. Kennelijk doe je daar 'iets vergelijkbaars'. Je kijkt naar r bij 0,8413 en r bij 0,1586 en berekent daarmee de standaarddeviatie en kennelijk kan je hier de standaarddeviatie uitrekenen door r_84.13% en r_15,86% te delen en dan de wortel te nemen... en dat zou je uit de formules moeten kunnen afleiden...

Zie Log-normal distributions [http://www.asp.ucar.edu/colloquium/1992/notes/part1/node105.html]

WvR
24-8-2003