WisFaq!

Tweede graadsvergelijkingen

Hoi,
ik heb aan m'n schoonzusje beloofd dat ik haar zou helpen en haar zou uitleggen
hoe je tweedegraadsvergelijkingen moet oplossen.
Alleen is het voor mij al 10 jaar geleden.

Dit is de opgave:de som van 2 opeenvolgende natuurlijke getallen is 481.
Bepaal die getallen.

Dit is tot waar ik ben geraakt met m'n oplossing:

x²+y²=481
x=y+1

(y+1)²+y²=481
x=y+1

(y²+2y+1²)+y²=481
x=y+1

2y²+2y+1=481
x=y+1

2y²+2y-480=0
x=y+1

y²+y-240=0
x=y+1

Alvast bedankt voor mij te helpen!!

Weten jullie evt. ook waar ik een cursus over tweede graadsvergelijkingen
kan vinden, zodat ik mijn wiskunde kan opfrissen en mijn schoonzusje kan uitleggen
hoe ze haar andere 7 opgaven moet oplossen. Zodat ze het ook onder de knie heeft voor haar
herexamen eind augustus.

mvg,
Sandra

Sandra Sicora
30-7-2003

Antwoord

Beste Sandra,

Waarom gebruik je een 2^degraadsvergelijking? Je moet de som van twee opeenvolgende natuurlijke getallen bepalen, en die moet gelijk zijn aan 481.
Noem het eerste getal x en het tweede getal x + 1 (want de getallen moeten opeenvolgend zijn), dan moet gelden
x + (x + 1) = 481
x + x + 1 = 481
2x + 1 = 481
2x = 481 - 1
2x = 480
x = 240

Dus het eerste getal is 240 en het tweede getal is 241, ter controle 240 + 241 = 481.



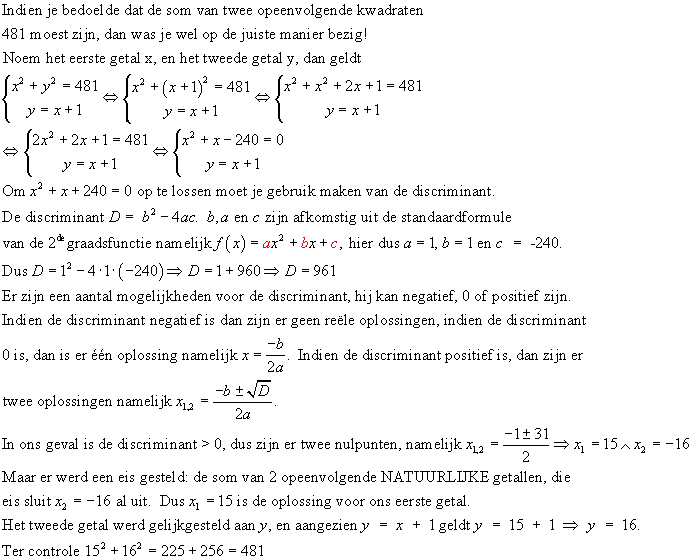
P.S. Ik heb hier gebruikgemaakt van de discriminant om x² + x - 240 = 0 te berekenen, maar je kon ook gebruik maken van 'ontbinden in factoren', met name de 'som-product-regel', die zegt "zoek twee getallen die opgeteld de coëfficiënt van de eerstegraadsterm zijn, maar het product van deze twee getallen is de constante term", als je lang genoeg had gezocht vond je (x - 15)(x + 16) = 0, want opgeteld zijn -15 + 16 = 1 en vermenigvuldigd zijn (-15)*16 = -240. En van (x - 15)(x + 16) = 0 de nulpunten berekenen is niet moeilijk, want een product is 0 dan en slechts dan als één van de factoren 0 is, dus x - 15 = 0 of x + 16 = 0 en hieruit volgen de nulpunten.

Groetjes,

Davy.

Davy
30-7-2003