WisFaq!

Opgaves met een kegelvlak

L.S.

Kunt u mij helpen met een opgave. Ik heb een kegelvlak K: y²=3(x²+z²) en het vlak V: y=2Ö3.

a) Allereerst moet ik bewijzen dat V en K elkaar snijden volgens een cirkel.

Voor mijn gevoel kan de cirkel alleen maar ontstaan als V en K loodrecht op elkaar staan. De normaalvectoren van V en K moeten dan elkaars tegenover gestelde zijn, echter ik kan dit niet ontdekken.

b) Vervolgens raakt een bol B K zodanig dat de raakcirkel in V ligt. Van deze B moet de straal berekend worden.

Ik zie niet in hoe men dit kan.

Kunt u mij helpen met deze 2 vragen?

Sebastiaan
29-7-2003

Antwoord

a) Alle punten die zowel op K als op V liggen voldoen aan de vergelijking (2Ö3)² = 3(x²+z²) of dus x²+z² = 4. Samen met y=2Ö3 is dat de vergelijking van een cirkel met middelpunt (0,2Ö3,0) en straal 2.

b) V en K hebben de cirkel uit punt a) gemeen. De genoemde raakcirkel C is wat B en K gemeen hebben (per definitie) en moet ook in V liggen (gevraagd). De raakcirkel is dus gewoon de cirkel uit het punt a).

Schets de situatie in het vlak x=0. De kegel wordt daar voorgesteld door de rechten y = ±Ö3 z.



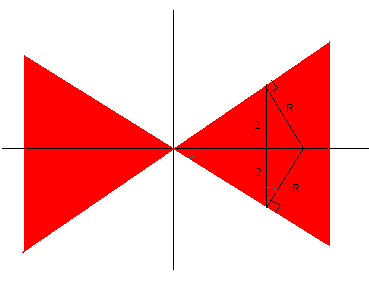
De aangegeven hoek is arctan(Ö3) = p/3. De straal wordt dus gegeven door 2/cos(p/3) = 4.

cl
29-7-2003