WisFaq!

Meetkunde

Ik ben een ingangexamen aan het invullen, maar ik heb er geen oplossingen van. Kan iemand mij helpen om deze vraag op te lossen?

Gegeven:
de rechte aa' evenwijdig met de Y-as, de punten b(2,5) en c(8,3), de hoek tussen het lijnstuk aa' en ab is b=30° en de hoek tussen het lijnstuk aa' en ac is a=45°

Gevraagd:
geef de coördinaten van het punt a (vierkantswortels moet je niet uitreken)

annelies
30-6-2003

Antwoord

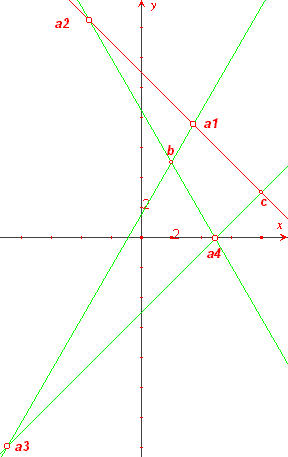
De lijn aa' is evenwijdig met de y-as. De hoek tussen aa' en een andere lijn is dus gelijk aan de hoek tussen die lijn en de y-as.
De hoek tussen een lijn en de x-as bepaalt de richtingscoëfficiënt van die lijn.

tan(90-30) = tan(60) = Ö3
tan(90-45) = tan(45) = 1

ab: y - 5 = Ö3 . (x - 2)
ac: y - 8 = 1 . (x - 3)

En hieruit kan het snijpunt a gevonden worden.

Maar let op: de hoek tussen twee lijnen is gedefinieerd als de SCHERPE hoek.
Er zijn dus meer mogelijkheden (zie figuur).

dk
1-7-2003