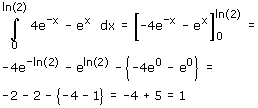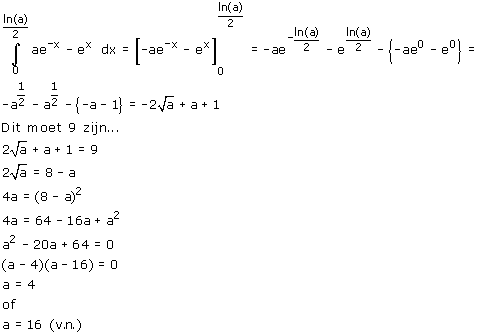WisFaq!

Buigpunten en oppervlakte

Ik heb een opgave die ik niet begrijp, en ik hoop dat jullie hem kunnen beantwoorden!

Namelijk:
Voor a1 is gegeven de familie functies f(x) = a·e^-x - e^x

1. Laat met een berekening zien dat voor a=4 de grafiek van f de x-as snijdt in het punt (ln2,0).
2. Bereken voor a=5 de coordinaten van het buigpunt van de grafiek van f.
3. Bereken voor a=4 de oppervlakte van het gebied dat wordt ingesloten door de x-as, de y-as en de grafiek van f.
4. Bereken de waarde(n) van a waarvoor de oppervlakte van het gebied dat wordt ingesloten door de x-as, de y-as, en de grafiek van f gelijk is aan 9?

Ik snap deze hele opgave niet, ik zou het heel fijn vinden als jullie hem beantwoorden. Alvast heel erg bedankt. Groetjes M.

Maritha Doornenbal
28-6-2003

Antwoord

1. 4e^-x-e^x=0
   e^-x(4-e^2x)=0
   4-e^2x=0
   e^2x=4
   2x=ln(4)
   x=ln(2)
   
   
2. f(x)=5e^-x-e^x
   f'(x)=-5e^-x-e^x
   f''(x)=5e^-x-e^x
   f''(x)=0
   Zie a.
   x=¹/₂·ln(5)
   
   
3. Omdat het hier gaat om het stuk ingesloten door de x-as, y-as en de grafiek van f moeten we kijken naar de integraal van f van 0 tot ln(2). (zie a.)
   
   
   
   
4. Nu dan het algemene geval:
   

Waarmee we wederom een opgave hebben opgelost.

WvR
28-6-2003