WisFaq!

Zijde en oppervlakte regelmatige achthoek

Hoe bereken ik de zijde en de oppervlakte van een regelmatige achthoek met als diameter 3m?

Dirk Spruyt
27-6-2003

Antwoord

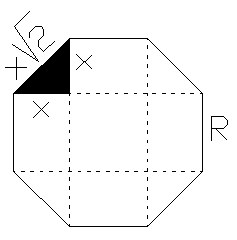
De regelmatig achthoek is te verdelen in een vierkant, vier gelijkbenige driehoeken en vier rechthoeken. Noem een been van de driehoek x, zodat de lengte van de hypotenusa is: √(x²+x²)=x√2 (Pythagoras). Nu geldt: R=x√2$\Leftrightarrow$x=¹/₂√2·R.
De diameter is 2x+R=R(1+√2)=3$\Leftrightarrow$R=3/(1+√2).
Het totaal oppervlak=4·(opp.(driehoek))+4·(opp.(rechthoek))+1·(opp.(vierkant)).
opp.(vier driehoeken)=4·(¹/₂·(¹/₂√2·R)²)=R²
opp.(vier rechthoeken)=4·(¹/₂√2·R²)=2√2·R²
opp.(vierkant)=R²
Dus het tot.opp.=2R²(1+√2)=2·(3/(1+√2))²·(1+√2)=18/(1+√2)=18(√2-1)

Sander
28-6-2003