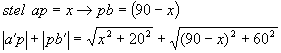
oplossen met de GR optie minimum geeft:
minimum
 120,42 voor x
120,42 voor x 22,50
22,50 Twee rechthoekige driehoeken staan met hun scherpe hoeken tegen elkaar en raken elkaar net in punt p zodat hun horizontale rechthoekszijden 1 rechte lijn vormen met maatgetal 90, de opstaande rechthoeszijde van de linker driehoek |aa'| meet 20 , die van de rechter |bb'| meet 60. Gevraagd wordt de kleinst mogelijke waarde van de som van hun schuine zijden |a'p|+|pb'| te berekenen. De juiste uitkomst zou 102,96 zijn. Ik kom door pythagoras toe te passen 131,77 uit, ik had |a'p| gelijk aan y gesteld en dan zo |pb'| in functie van y berekend , dat dan opgeteld en gelijk aan 0 gesteld waarna ik voor y 65,88 vond,wat niet de minimale waarde is. Kunnen jullie mij helpen ?berten
26-6-2003
Hallo Berten,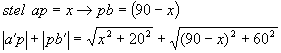
oplossen met de GR optie minimum geeft:
minimum120,42 voor x
22,50
wl
26-6-2003
#12820 - Vlakkemeetkunde - 3de graad ASO