WisFaq!

Wanneer heeft x³ + px -1 = 0 drie oplossingen?

Voor welke p's heeft x³ + p x - 1 = 0 drie oplossingen?
Hopelijk is dat voldoende
Groetjes

Compugreen
23-6-2003

Antwoord

Bekijk de afgeleide functie 3x²+p. Als p0 heeft deze geen nulpunten zodat de originele functie overal stijgt. Zelfde resultaat voor p=0.

We willen eigenlijk dat de functie van -¥ komt, nul wordt in een bepaald punt, verder stijgt, zich omdraait en begint te dalen, weer nul wordt, zich weer omdraait en begint te stijgen, en zo een derde keer nul wordt alvorens in de +¥-heid te verdwijnen.

p0 is daar al een vereiste voor, maar het zou ook kunnen dat dat hele draai-en-keer-proces zich afspeelt zwevend boven of onder de x-as en op die manier toch nog steeds voor slechts één nulpunt zorgt.

Een bijkomende vereiste is dus dat de functiewaarde in het minimum kleiner is dan nul en de functiewaarde in het maximum groter is dan nul.

x(max) = -Ö(-p/3)
x(min) = +Ö(-p/3)

f(x(max)) = (2/9)Ö(-p³/3)-1
f(x(min)) = -(2/9)Ö(-p³/3)-1

Aangezien f(x(max)) toch groter zal zijn dan f(x(min)) kan je nu even goed eisen dat f(x(max)).f(x(min)) kleiner moet zijn dan nul (wat betekent dat ze een verschillend teken hebben)

4p³/27 + 1 0

Dat is alleen zo als p -3.2^-2/3 -1,89. Deze eis overtreft de eerste (p0) en blijft dus als enige over.

Hieronder een kleine animatie ter verduidelijking. De parameter p verandert hierbij van -8 tot 2. Je ziet eerst drie nulpunten, dan een omdat het maximum onder de x-as duikt en ten slotte is dat zelfs al de reden niet meer dat er maar een nulpunt is, de functie wordt gewoon monotoon stijgend...

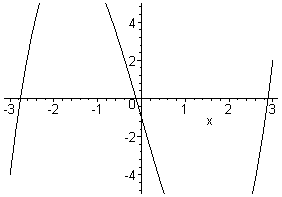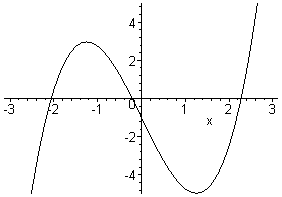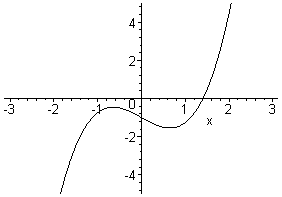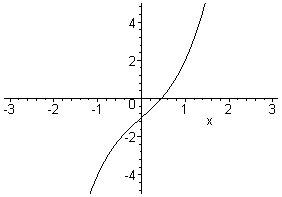
cl
23-6-2003