WisFaq!

Integreren+oppervlakte

Na lang probreren kom ik hiet echt niet uit.
Ik moet de oppervlakte berekenen van de ingesloten figuur tussen de krommen

Y= (x-1)² , Y=9 Y= 2x+1

Wie kan mij hiet mee helpen 't is een oude examen vraag, ik wil zo veel mogelijk oefenen.

Alvast heel erg bedankt
Mirella

Mirella
17-6-2003

Antwoord

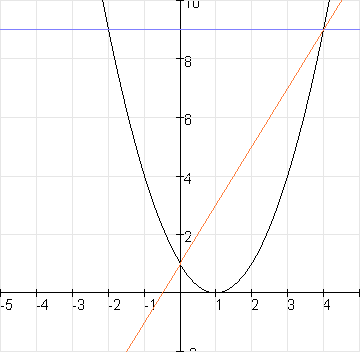
Deze integraal kun je opsplitsen in twee stukken: het traject van -2 tot 0 en het traject van 0 tot 4.
Het opp. behorend bij het eerste traject krijg je door de parabool y=(x-1)² tijdelijk 9 stappen naar beneden te transleren en dan te integreren.
Je gevraagde oppervlakte ligt dan immers beneden de y-as.
(let daarbij op dat je ook je integratiegrenzen omkeert want anders krijg je een negatieve oppervlakte.

Het oppervlak behorend bij het 2e traject is 'simpelweg' de oppervlakte van de driehoek waarvan de punt naar beneden wijst. met basis 4 en hoogte 8.
De som van deze twee deel-oppervlaktes levert je de totale oppervlakte.

groeten,
martijn

mg
17-6-2003