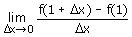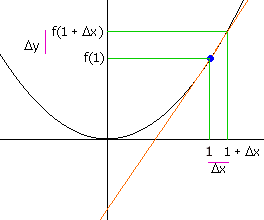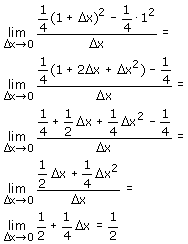WisFaq!

Exact berekenen

Gevraagd: de veranderingssnelheid in A (1,1/4)
Gegeven: f(x) = 1/4 x tot de tweede

Stap 1:
D Y / D x (1,1 + D X) = f(1 + D x)- f(1) / (1 + D X) - 1 = 1/2 D x + 1/4 (D X)tot de tweede / D x = 1/2 + 1/4 D x
Stap 2:
voor Dx -- 0 vinden we (dy / dx)x=1 = 1/2

Dit is een voorbeeld in ons boek. Ik snap er niets van ik zou graag wat meer duidelijk heid wilen alvast bedankt (D) = delta

Wendy
14-6-2003

Antwoord

Om de veranderingssnelheid (zeg maar de richtingscoëfficiënt van de raaklijn) in een punt te berekenen kan je het differentiequotient bepalen is dat punt. Dit doe je door Dx naar nul te laten naderen:



Je moet nu even goed kijken wat er staat!



Kortom daar staat niets anders als Dy/Dx waarbij je Dx naar nul laat naderen.

f(1+Dx) en f(1) kan je uitrekenen door dit in het functievoorschrift in te vullen en verder te vereenvoudigen. Kijk maar eens:



Hopelijk is het met de tussenstappen erbij duidelijker. Zo niet... dan horen we het wel weer.

WvR
14-6-2003