WisFaq!

Hoe integreren

f(x)= x³-x² en g(x)= 2x

Gevr.a) teken de grafiek van beide functies
b) Bereken de oppervlakte van de door de grafieken ingesloten vlakdelen.

Nu is het niet moeilijk om de grafieken te tekenen maar Bij vraag b krijg ik als antwoordt -4 2/3 wat dus zeer fout is..oppervlakte kan nooit negatief zijn. Zo heb ik dit aangepakt:

g(x)-f(x)= 2x-x³-x², En die dan geintegreerd en toen kreeg ik dit:

2 Inte.teken 0 tot met 2 x²/2 - x^4/4 - x^3/3 dx

En toen kreeg ik door 2 en o in te vullen en 0 aftrekken van de waarde van 2.

-4 2/3.

Maar wat ik ook niet snap is dat ze deze integraalformule niet geven 1/1+n x^1+n dit geven ze in een van de volgende paragrafen, dus misschien moet men het heel anders aanpakken.

Zou u deze sommetje aub willen laten zien ,want ik begrijp er niets van.

En wanneer moet men dan wel die formule gebruiken ?

Tim
9-6-2003

Antwoord

Hoi,

Ik heb de situatie even getekend.

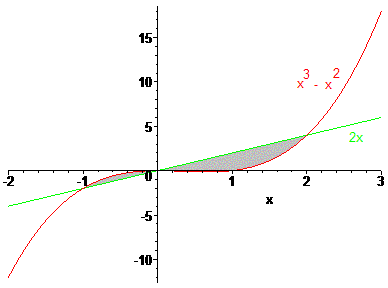
Er zijn twee oppervlaktes die je moet berekenen. Eentje ligt onder de x-as en de andere ligt grotendeels boven de x-as (een klein gedeelte onder de x-as). Je moet eerst de snijpunten bepalen omdat je moet weten welke integratie-intervallen je moet nemen.
f(x) = g(x) Û x³ - x² = 2x Û x³ - x² - 2x = 0 Û x(x² - x - 2) = 0 Û x = 0 Ú x² - x - 2 = 0.
Dit laatste kun je berekenen m.b.v. discriminant, x₁ = -1, x₂ = 2 Þ snijpunten zijn x = -1, x = 0, x = 2.

De oppervlakte gebied onder x-as gaat van -1 tot 0. Je moet telkens de bovenste grafiek - de onderste als integrand nemen.


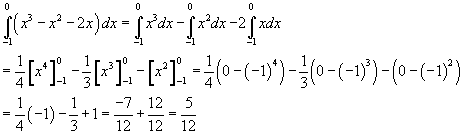
Bij het bepalen van de oppervlakte van het volgende gedeelte ligt de groene grafiek boven de rode, dus wordt de integrand (2x - (x³-x²)). Het integratie-interval is van 0 tot 2.


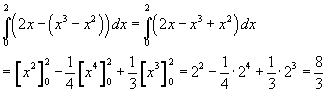
Dus oppervlakte vlakdelen ⁵/₁₂ + ⁸/₃ = ³⁷/₁₂ 3,08333...

Indien iets onduidelijk is, kun je reageren op dit antwoord.

Groetjes,

Davy.

Davy
9-6-2003