Maar nu terzake. Veel hangt af van de juiste locatie van de steden ten opzichte van elkaar. Neem aan dat alle steden zich op een perfecte cirkel bevinden en evenver van elkaar. Elk punt kan dan gekozen worden want de som van de kilometers tot elk bedrijf is dan voor elk punt binnen de cirkel minimaal. Anders is het als de bedrijven niet evenver van elkaar liggen. Bvb 10 steden in de bovenste cirkelhelft, en slechts 1 stad in de onderste. Het is dan logisch dat het distributiecentrum in de bovenste helft zich zal lokaliseren om de totale kilometers te minimeren.
Iets soortgelijks zie je op onderstaande tekeningen.
Bij 2 steden, kan je weer elk punt nemen, maar het middelste is het meest logische.
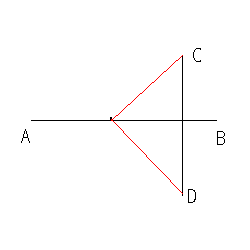
Bij 4 steden, is het wel duidelijk te stellen waar het optimale punt ligt, namelijk op het snijpunt van de 2 rechten. Zouden we het oude punt nemen, dan kan je zien dat de rode lijnen langer zijn dan de rechtstreekse verbinding.
Nu gaan we hetzelfde doen met de 11 steden. We gaan ze beschouwen als een veelhoek om zo het midden te bepalen. Ofwel gebruik je een landkaart, ofwel gebruik je dezelfde verhoudingen (als je het aantal kilometers tussen de steden kent en dus de zijden). Nu moet je de overstaande steden met elkaar verbinden en op de plaats waar de meeste lijnen samenkomen kan je best je distributiecentrum plaatsen. Heb je een paar punten waar veel lijnen samenkomen, moet je daar weer het midden van bepalen.
Nu, er is een probleem als er steden buiten onze 'geografische cirkel' liggen. Van daaruit een lijn trekken heeft weinig invloed, want het zal er niet voor zorgen dat het centrum dichter bij deze stad komt te liggen. Stel dat dit maar bij 1 stad is, kan je het nog eenvoudig oplossen. Ligt deze stad bvb 10 km buiten de cirkel dan moet het centrum met 10 km * 1/11 verplaatsen richting deze 11de stad.
Je merkt misschien al dat dit laatste te vergelijken is met een vector. En zo kan je het ook benaderen als je er goed mee overweg kunt. Je kan de steden zetten in een assenstelsel. Voor de stad het meest in het Zuidwesten kan je dan de co÷rdinaat (0,0) meegeven. De co÷rdinaten van de anders steden kan je dan vinden door de afstand in respectievelijk westelijke en noordelijke richting te nemen. Je kan natuurlijk ook de echte lengte- en breedtegraden nemen, maar dat zou ons te ver leiden denk ik.

Dan neem je een willekeurig punt als 'virtueel centrum' en van dat punt bereken je de afstand tot de 11 steden. Dit is dan de grootte van de vector. Door de gebruikelijke bewerkingen met vectoren (door de vectoren eigenlijk te laten inwerken op dit punt) verschuift dit punt naar de meest centrale plaats. Dit is trouwens de manier waarop een routeplanner werkt. In het programma zit een afstandenmatrix (hoeveel km van A tot B) en de co÷rdinaten van de steden. Een soortgelijke manier kan je dus zelf ook gebruiken.
Bemerk dat dit nog steeds een benadering zal zijn van de werkelijkheid, want de wegen volgen nooit de kortste weg. Ook heb je nog verschillen tussen 50 km over de autosnelweg of 50 km via kleine dorpjes. En nog heel wat andere dingen waarmee in de praktijk rekening wordt gehouden, wat je via de wiskunde of de computer niet kunt berekenen.
Ik hoop dat dit een idee geeft, en dat jullie verder kunnen.
Groetjes,
Tom
tg
30-5-2003