WisFaq!

Re: De kegel met de grootste inhoud

hallo,
ik snap niet echt hoe je aan die tan komt enzo..
maar je moet met behulp van deze formule:
2 pi keer de straal (de straal is 10)
en dat keer 10/360
10 graden is de overlappingshoek van de kegel en 360 heeft de kegel helemaal.
nou veranderen we steeds de overlappingshoek ( dus 10 graden wordt bijv. 20, 30, 40 enzo.)
dan krijg je de formule:
2 pi · R- ( 2 pi · R · (x/360)
en x is aantal graden ( overlappingshoek)
met deze formule moet je de inhoud en de hoogte bereken
want de hoogte weet je ook niet.
alvast bedankt

marloes
26-5-2003

Antwoord

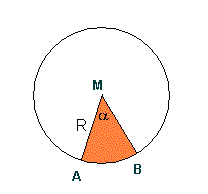
Je begint dus met een cirkel, met straal R, en daar knip je een bepaalde 'taartpunt' uit (het stuk M-A-B).
Dit is hetzelfde als de overlappingshoek waar jij over spreekt.
Wanneer je nou de randen MA en MB weer aan elkaar plakt, dan krijg je een kegel. (als je teveel drinkt, ook trouwens )

Vergelijk nou bovenstaand plaatje eens met onderstaand plaatje:

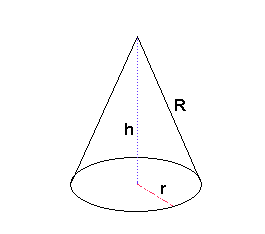
De schuine zijde van de kegel is hetzelfde als de straal R (let wel: de grote 'R') van de cirkel.
Merk verder op dat de omtrek van het grondvlak van de kegel (2$\pi$r) hetzelfde is als de omtrek van de cirkel waar we mee begonnen zijn (2$\pi$R) maar dan met weglating van het stukje AB.
Dit stukje AB is $\alpha$/360 e deel van 2$\pi$R.
Dus er geldt dat 2$\pi$r=2$\pi$R - ($\alpha$/360).2$\pi$R

nu eerst even links en rechts 2$\pi$ wegstrepen:
r=R-($\alpha$/360).R $\Leftrightarrow$ r=R.(1-$\alpha$/360)

Omdat r, h, en R een rechthoekige driehoek vormen, ben je in staat om mbv Pythagoras de hoogte h uit te rekenen:
R²=r²+h² $\Leftrightarrow$ h²=R²-r² $\Leftrightarrow$ h=√(R²-r²)

De inhoud van de cilinder = ¹/₃.Grondvlak.hoogte
Grondvlak= $\pi$r²
Dus I=¹/₃.$\pi$r².√(R²-r²)

groeten,
martijn

mg
27-5-2003