WisFaq!

Vierdegraads vergelijkingen

hallo, ik heb op een site het volgende gelezen:
Now, we can write:

y4+py2=-qy-r
y4+2py2+p2=py2-qy-r+p2
(y2+p)2=py2-qy-r+p2.

Now, for any z,

(y2+p+z)2=((y2+p)+z)2
=(y2+p)2+2(y2+p)z+z2
=py2-qy-r+p2+2z(y2+p)+z2
(p+2z)y2-qy+(p2-r+2pz+z2) (*)

The right hand side of (*) is a quadratic in y; and we can choose z so that it is a perfect square, ie so that the discriminant is zero, ie:

(-q)2-4(p+2z)(p2-r+2pz+z2)=0.

We can rewrite this as (q2-4p3+4pr)+(-16p2+8r)z-20pz2-8z3=0.

het eerste snap ik nog, maar dan vanaf now any z. Hoe doen ze dat allemaal in z schrijven en wat bedoelen ze met de right hand?
Zou u zo spoedig mogelijk willen terugschrijven ivm deadline!!!
Alvast bedankt

.
18-5-2003

Antwoord

Eerst nog even het stukje dat je snapte

Let goed op de rode kleur)



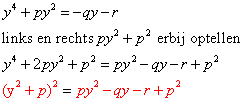
Nu het tweede gedeelte


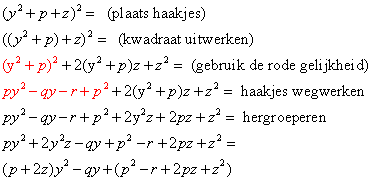
dit is van de vorm
ay²+by+c

Right hand side is engels voor "rechterlid",
hier gewoon de laatste regel
De discriminant van deze uitdrukking is:
(-q)²-4(p+2z)(p²-r+2pz+z²

Nu willen ze dat die discriminant 0 is zodat uitdrukking *
een kwadraat is.
Kun je zo verder?

hk
18-5-2003