WisFaq!

Oppervlakte van een afgeknotte cirkel

Okay, stel je hebt een cirkel met een omtrek van 25 (cm bijvoorbeeld). Deze cirkel vergroot je met X, dus de omtrek van de cirkel wordt 25+x (nogal logisch). Nu wordt het iets lastiger uitleggen.

De lengte x bevindt zich aan de bovenkant van de circel.
Er komt een horizontale lijn door de circel heen, die zich dus op de hoogte van waar x ophoudt en begint bevindt.
Het gaat nu om de oppervlakte van de 'afgeknotte' cirkel.
hmm.. ik hoop dat het werkt maar dit plaatje zou het ongeveer moeten weergeven:

Jonathan
7-5-2003

Antwoord

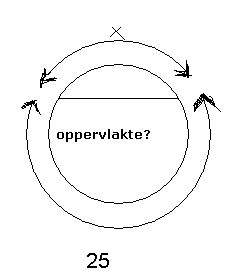
De oppervlakte S van de afgeknotte cirkel kan geschreven worden als (zie figuur)

S = Opp(cirkel) - Opp(sector) + Opp(driehoek)



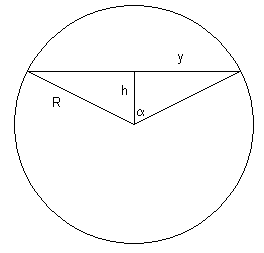
Opp(cirkel) = pR²
Opp(sector) = aR²
Opp(driehoek) = y·h = R sin(a) R cos(a) = (R²/2) sin(2a)

Combineren we dat met de relaties (waarin L de originele omtrek voorstelt, dus L=25 in jouw voorbeeld)

R = (L+x)/(2p)
a = x/(2R)

dan krijgen we uiteindelijk

S(x) = (L+x)/(8p²)·[2pL + (L+x)·sin((2px)/(L+x))]

Merk op dat, zoals verwacht,

S(0) = L²/(4p) = pR(0)² (afgeknot = volledig)
S(L) = L²/(2p) = pR(L)²/2 (afgeknot = volledig/2)
S(¥) = 0

Je kan aantonen dat de waarde S(L) het maximum is van S(x). Hieronder zie je de grafiek van S(x) voor het geval L=25 (de grafieken voor andere waarden van L zijn hier gelijkvormig mee).

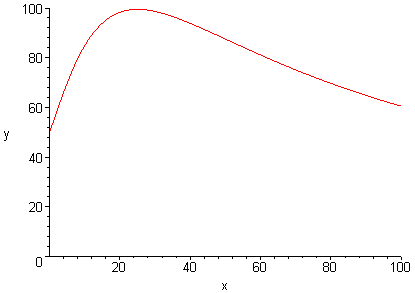
Let wel, het maximum is hier niet 100, maar wel

625/(2p) = 99,47183941 :-)

cl
7-5-2003