WisFaq!

Rank

Ik heb een matrix

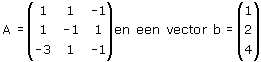
Ik weet dat de rank(A)=2, omdat er 2 pivots in zitten. Volgens het boek is de rank(A|b) ook gelijk aan 2. Ik begrijp niet hoe dit berekent wordt. Kunt u mij dit uitleggen en kunt u mij een geval tonen waarbij rank(A) ongelijk is aan rank(A|b)?

Hartelijk dank.

Jos
5-5-2003

Antwoord

De rang wordt gedefinieerd als het aantal niet-nulrijen na Gauss-Jordan rijreductie van een matrix. Of die matrix vierkant is of niet doet dus niet terzake.

Rang(A|b) is niet noodzakelijk gelijk aan rang(A). De matrix

1 0 0
0 4 0
0 0 0

heeft bijvoorbeeld rang 2,

1 0 0 3
0 4 0 5
0 0 0 0

ook, maar

1 0 0 3
0 4 0 5
0 0 0 1

heeft rang 3. Dat laatste komt natuurlijk overeen met een strijdig stelsel. Je ziet dus dat de b-vector wel degelijk invloed heeft op de rang van A|b.

cl
5-5-2003