WisFaq!

Re: Wat is de primitieve van x^x?

Volgens dr. Math bestaat deze niet. Dan ben ik benieuwd of er ook bewijs van is dat er geen functievoorschrift voor is. Ik ben nu namelijk er mee bezig om dat te zoeken (hopend dat het nog niet bestaat) net als de afgeleide van f(x)^g(x).

Maikel
5-5-2003

Antwoord

Ik wil je enthousiasme niet drukken, maar de wiskunde is ondertussen zodanig uitgebouwd dat de kans zeer klein is dat je als HBO-student een wezenlijke bijdrage zou kunnen leveren.

Stel f(x) = x^x, x0.



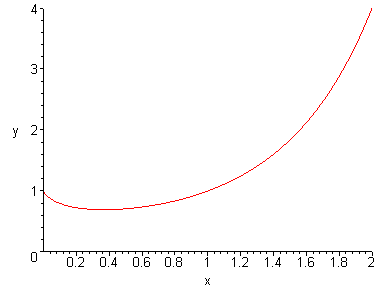
We zoeken dus een functie F(x) waarvoor F'(x) = f(x). Die functie noemen we een primitieve functie van f(x) en dit is er zo een.



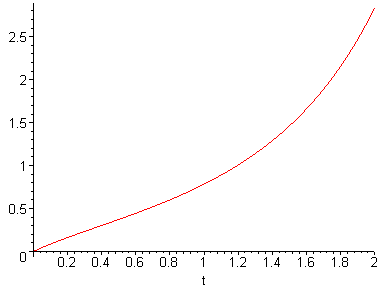
Helaas kan je die functie niet zomaar neerschrijven als een combinatie van elementaire functies (rationale functies, exponentielen, logaritmes, goniometrische en cyclometrische functies), maar je ziet, ze *bestaat* wel.

Wat je wel kan doen is voor die functie een oneindige reeks opschrijven, die je in staat stelt om de functiewaarde van F(x) te berekenen voor om het even welke x. En eigenlijk is dat niet zo erg. Een dergelijke reeks-oplossing is zeker niet minder waard dan een expliciete uitkomst als bijvoorbeeld "sin(x)", want in dat laatste geval weet je ook niet wat nu precies de waarde is van sin(0.43534). Je rekenmachine maakt voor sin(x) trouwens ook gebruik van dergelijke reeksen.

Wat misschien wel theoretisch mogelijk is, is aantonen dat er geen (eindige) combinatie van elementaire (zie boven) functies bestaat, die na afleiding, x^x zou opleveren, maar dat lijkt me *zeer* ver buiten het bereik van deze site.

cl
7-5-2003