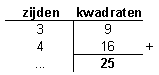Pythagoras werd geboren in Samos ca. 575 v.C. - waarschijnlijk Metapontum, Zuid-Italië, na 500 v.C. Pythagoras staat bekend als Grieks wijsgeer en hervormer, een van de meest raadselachtige figuren uit de geschiedenis van het Griekse denken.
Omstreeks 530 v.C. stichtte Pythagoras in Croton een school, die ook in andere Zuiditalische steden afdelingen vestigde. Pythagoras en zijn aanhangers hebben een belangrijke invloed uitgeoefend op het openbare en het politieke leven, maar zijn daarbij ook op krachtig verzet gestuit; tegen het eind van zijn leven moest Pythagoras Croton verlaten en enkele decennia later vond een algehele opstand tegen zijn aanhangers plaats.
De oorspronkelijke getallenleer van Pythagoras en de zijnen was geen wetenschappelijke wiskunde, maar eerder een toepassing, een soort metafysica van het getal; op den duur is echter ook in de school van Pythagoras, net als op andere plaatsen in de Griekse wereld, wiskunde op wetenschappelijke wijze beoefend. Hun voornaamste bijdrage ligt op het gebied van de getallenleer, terwijl zij de meetkunde in het algemeen op 'aritmetische' wijze beoefenden en daardoor onder meer geen raad wisten met het probleem van de irrationele wortels.
Uit: Encarta(R) 99 Encyclopedie Winkler Prins Editie.
Meer informatie over pythagoras:
De stelling van Pythagoras
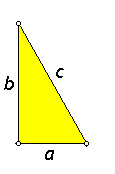 De stelling van Pythagoras is waarschijnlijk de meest bekende stelling in de wiskunde. De stelling zegt iets over de relatie tussen de rechthoekszijden en de schuine zijde van alle rechthoekige driehoeken.
De stelling van Pythagoras is waarschijnlijk de meest bekende stelling in de wiskunde. De stelling zegt iets over de relatie tussen de rechthoekszijden en de schuine zijde van alle rechthoekige driehoeken.
In de rechthoekige driehoek ABC zijn de zijden a en b de rechthoekszijden. De zijde c noemen we de schuine zijde of hypotenusa.
De stelling van pythagoras luidt:
'In een rechthoekige driehoek is het kwadraat van de hypotenusa gelijk aan de som van de kwadraten van de rechthoekszijden.'
Anders geformuleerd: a2 + b2 = c2
De stelling van Pythagoras is één van de oudste stellingen uit de oudheid. De stelling is genoemd naar de Griekse wiskundige en filosoof Pythagoras . Volgens de legende was Pythagoras zo is z'n nopjes met de ontdekking van de stelling dat hij een offer aan de goden bracht in de vorm van een paar ossen.
Er zijn vele bewijzen van de stelling van Pythagoras bekend.
Een bekend en makkelijk te onthouden bewijs is het volgende:

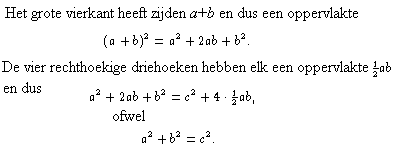
Meer informatie is te vinden op:
Voorbeeld
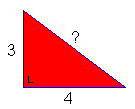 Hier zie een (bekende?) rechthoekige driehoek staan. Om de schuine zijde uit te rekenen kun je gebruik maken van een rekenschema:
Hier zie een (bekende?) rechthoekige driehoek staan. Om de schuine zijde uit te rekenen kun je gebruik maken van een rekenschema:

Eerst vul je de zijden die je weet in en bereken je de kwadraten:

Je weet dat de som van de kwadraten van de rechthoekszijden gelijk moet zijn aan het kwadraat van de schuine zijde. Daarmee kan je het ontbrekende kwadraat uitrekenen.
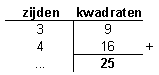
Je kent nu het kwadraat van de schuine zijde. De schuine zijde is de wortel van 25 en dat is 5. De schuine zijde is 5.
Oefeningen
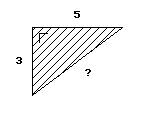
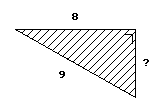
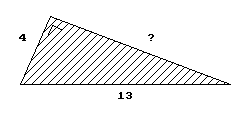
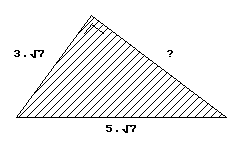
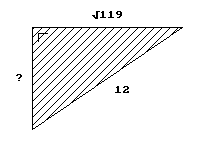
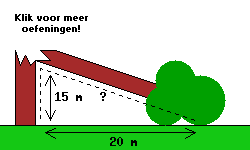
Bereken bij de driehoeken hieronder eerst zelf de onbekende zijde.
Als je op de driehoek klikt kun je zien of je het goed gedaan hebt.
F.A.Q.
Antwoorden en toets...






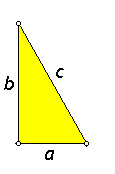 De stelling van Pythagoras is waarschijnlijk de meest bekende stelling in de wiskunde. De stelling zegt iets over de relatie tussen de rechthoekszijden en de schuine zijde van alle rechthoekige driehoeken.
De stelling van Pythagoras is waarschijnlijk de meest bekende stelling in de wiskunde. De stelling zegt iets over de relatie tussen de rechthoekszijden en de schuine zijde van alle rechthoekige driehoeken.
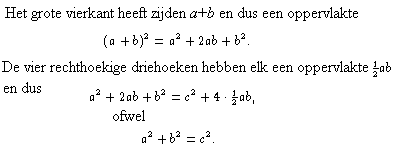
 Hier zie een (bekende?) rechthoekige driehoek staan. Om de schuine zijde uit te rekenen kun je gebruik maken van een rekenschema:
Hier zie een (bekende?) rechthoekige driehoek staan. Om de schuine zijde uit te rekenen kun je gebruik maken van een rekenschema: