|
|
|
\require{AMSmath}




Functie voorschrift hyperbool bij 3 punten
De standaardfunctie voor de grafiek van een hyperbool.
$ \eqalign{f(x) = \frac{1} {{p\left( {x - q} \right)}} + r} $
Voorbeeld
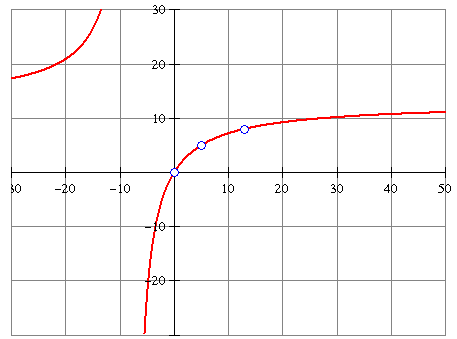
Geef de formule voor de hyperbool door de punten A(0,0), B(5,5) en C(13,8).
Uitwerking
$ \eqalign{ & f(x) = \frac{1} {{p\left( {x - q} \right)}} + r \cr & 1.\,\,\frac{1} {{p\left( {0 - q} \right)}} + r = 0 \Rightarrow - \frac{1} {{pq}} + r = 0 \cr & 2.\,\,\frac{1} {{p\left( {5 - q} \right)}} + r = 5 \cr & 3.\,\,\frac{1} {{p\left( {13 - q} \right)}} + r = 8 \cr & Oplossen\,\,geeft: \cr & p = - \frac{{25}} {{2496}},\,\,q = - \frac{{39}} {5}\,\,en\,\,r = \frac{{64}} {5} \cr} $
Naschrift
Ik geloof dat ik deze formule als standaardhyperbool wel zo handig vind:
$ \eqalign{f(x) = \frac{p} {{\left( {x - q} \right)}} + r} $



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|







