Frequentie-tabel
Voorbeeld
Hieronder zie de resultaten van een proefwerk wiskunde:
9, 7, 5, 6, 8, 3, 8, 7, 5, 6, 5, 6, 4, 9, 4, 7, 6, 6, 7, 8, 5, 2, 6, 7 en 6
Om een goed overzicht te krijgen over de resultaten kan je de gegevens in een frequentie-tabel zetten. Dat wordt dan een lijstje met per cijfer het aantal keren dat het cijfer voorkomt.
|
r |
aantal |
 2 2 |
 .. .. |
 3 3 |
 ... ... |
 4 4 |
 ... ... |
 5 5 |
 ... ... |
 6 6 |
 ... ... |
 7 7 |
 ... ... |
 8 8 |
 ... ... |
 9 9 |
 ... ... |
|
|
r |
aantal |
 2 2 |
 | | |
 3 3 |
 | | |
 4 4 |
 || || |
 5 5 |
 |||| |||| |
 6 6 |
 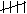 || || |
 7 7 |
 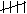  |
 8 8 |
 ||| ||| |
 9 9 |
 || || |
|
|
r |
aantal |
 2 2 |
 1 1 |
 3 3 |
 1 1 |
 4 4 |
 2 2 |
 5 5 |
 4 4 |
 6 6 |
 7 7 |
 7 7 |
 5 5 |
 8 8 |
 3 3 |
 9 9 |
 2 2 |
|
|
tabel maken |
turven |
tellen |
Vervolgens kan je deze gegevens in een staaf- of lijngrafiek weergeven, zodat je nog een beter 'beeld' krijgt van de verdeling:

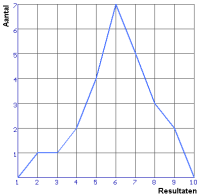
Absolute en relatieve frequentie
In het voorbeeld hierboven hebben de absolute frequenties gebruikt. Dat wil zeggen de 'echte' aantallen zoals deze in de populatie of steekproef voorkomen. Soms zijn we meer geinteresseerd in de aantallen in vergelijking met het totaal aantal. We spreken dan van relatieve frequenties. Meestal zijn dit procenten...
\eqalign{relatieve\,frequentie=\frac{frequentie}{totale\,frequentie}\times100\%}
|
resultaten |
aantal |
 2 2 |
 1 1 |
 3 3 |
 1 1 |
 4 4 |
 2 2 |
 5 5 |
 4 4 |
 6 6 |
 7 7 |
 7 7 |
 5 5 |
 8 8 |
 3 3 |
 9 9 |
 2 2 |
|
|
resultaten |
aantal |
 2 2 |
 4% 4% |
 3 3 |
 4% 4% |
 4 4 |
 8% 8% |
 5 5 |
 16% 16% |
 6 6 |
 28% 28% |
 7 7 |
 20% 20% |
 8 8 |
 12% 12% |
 9 9 |
 8% 8% |
|
absolute
frequenties |
relatieve
frequenties |
Cumulatieve frequentie
Soms zijn we geinteresseerd in de som van de frequenties, de zgn. cumulatieve frequenties. De betekenis van deze cumulatieve frequentie is het aantal waarnemingen 'dat je tot dan toe hebt gehad'.
|
resultaten |
frequentie |
cumulatieve
frequentie |
 2 2 |
 1 1 |
 1 1 |
 3 3 |
 1 1 |
 2 2 |
 4 4 |
 2 2 |
 4 4 |
 5 5 |
 4 4 |
 8 8 |
 6 6 |
 7 7 |
 15 15 |
 7 7 |
 5 5 |
 20 20 |
 8 8 |
 3 3 |
 23 23 |
 9 9 |
 2 2 |
 25 25 |
|
|
resultaten |
relatieve
frequentie |
cumulatieve
relatieve
frequentie |
 2 2 |
 4% 4% |
 4% 4% |
 3 3 |
 4% 4% |
 8% 8% |
 4 4 |
 8% 8% |
 16% 16% |
 5 5 |
 16% 16% |
 32% 32% |
 6 6 |
 28% 28% |
 60% 60% |
 7 7 |
 20% 20% |
 80% 80% |
 8 8 |
 12% 12% |
 92% 92% |
 9 9 |
 8% 8% |
 100% 100% |
|
F.A.Q.







 ||
||
