Formules bij rechte lijnen

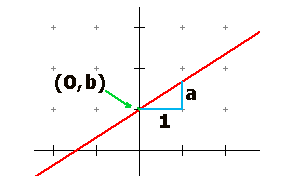Formule van een lijn door twee punten

Als een lijn door $A$ en $B$ gaat dan kan je ook op deze manier een vergelijking van die lijn opstellen:

• $\eqalign{a=\frac{y_B-y_A}{x_B-x_A}}$
• $\eqalign{f(x)=a(x-x_A)+y_A}$

Je kunt daarna het functievoorschrift schrijven in de standaardvorm. Een kwestie van haakjes wegwerken en de gelijksoortige termen samennemen.

---

Voorbeeld 1

---

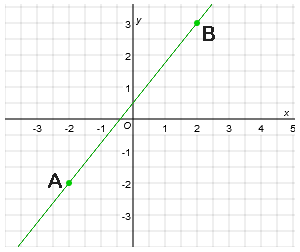
• $\eqalign{a=\frac{3--2}{2--2}=\frac{5}{4}=1\frac{1}{4}}$
• $\eqalign{f(x)=1\frac{1}{4}(x+2)-2}$

Toelichting

• In de formule is $a$ de richtingscoëfficient.
• In de formule hebben we in het stuk na de richtingscoëffiënt de coördinaten van $A$ ingevuld. Dat moet niet, je had ook de coördinaten van $B$ kunnen gebruiken:
  $\eqalign{f(x)=a(x-x_B)+y_B}$

---

Voorbeeld 2

---

De lijn $k$ gaat door het punt $A(5,-2)$ en heeft als richtingscoëfficiënt $a=-\frac{2}{3}$.

• $y=-\frac{2}{3}(x-5)-2$ is een goede vergelijking voor $k$.

---

Voorbeeld 3

---

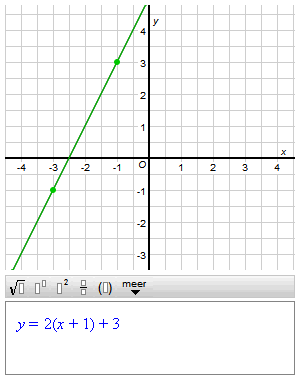
De lijn gaat door de punten $A(-3,-1)$ en $B(-1,3)$. De richtingscoëfficiënt is gelijk aan: $\eqalign{rc_l=\frac{-1-3}{-3--1}=\frac{-4}{-2}=2}$ Neem het punt B als 'steunpunt'. De vergelijking wordt dan: $y=2(x+1)+3$ Als je het punt A als 'steunpunt' neemt dan krijg je de vergelijking: $y=2(x+3)-1$ Maar dat is natuurlijk hetzelfde... toch?

Terug Home