1. Eigenschappen
Een magisch vierkant of tovervierkant is een dusdanige ordening van getallen in een vierkant, dat de som van de getallen voor elke rij, elke kolom en elke diagonaal gelijk is. Standaard worden hiervoor de getallen
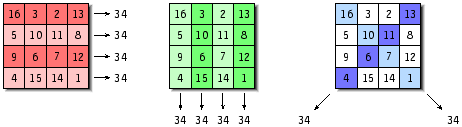
met toestemming overgenomen van www.magic-squares.de
Het aantal rijen/kolommen (standaard gelijk aan n) wordt de orde van het magisch vierkant genoemd.
De som van een rij/kolom/diagonaal wordt wel de magische constante, het karakteristiek getal of het tovergetal genoemd en is (in het standaard geval) gelijk aan
Immers de som van alle getallen van het tovervierkant is 1+2+...+(n2-1)+n2 = 1+n2 +2+(n2-1) + . . . =
Afgezien van het getal 1 (een 1 bij 1 vierkant) bestaat het eenvoudigste tovervierkant uit 3x3 getallen. De som van elke rij is dan 15. Een tovervierkant van orde 2 (met de getallen 1 t/m 4) is onmogelijk..
In de praktijk worden ook andere getallen gebruikt dan 1 t/m n2. Zo bestaan er tovervierkanten die uitsluitend uit kwadraten of uitsluitend uit priemgetallen bestaan. Dit soort tovervierkanten zijn dus niet zuiver. Soms laat men zelfs de eis dat de getallen verschillend moeten zijn vallen, zodat ook een vierkant met 16 enen magisch genoemd wordt. Dit soort vierkanten worden gebruikt bij de constructie van echte tovervierkanten.
Sommige tovervierkanten hebben wat extra's , zoals een 'pandiagonaal' magisch vierkant (ook wel panmagisch vierkant genoemd) . Daar leveren ook de 'subdiagonalen' steeds die zelfde som op: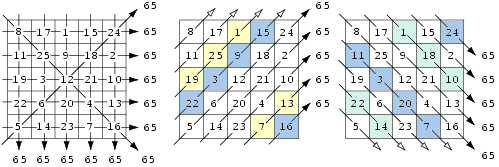
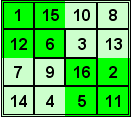 Bij een volkomen perfect magisch vierkant geldt (onder andere) dat binnen elke 2x2 deelvierkant de som der getallen gelijk is. In het voorbeeld hiernaast is is niet alleen de som van elke rij/kolom/diagonaal 34, maar ook de som van elk van de negen 2x2 vierkanten !
Bij een volkomen perfect magisch vierkant geldt (onder andere) dat binnen elke 2x2 deelvierkant de som der getallen gelijk is. In het voorbeeld hiernaast is is niet alleen de som van elke rij/kolom/diagonaal 34, maar ook de som van elk van de negen 2x2 vierkanten !
Andere extra eigenschappen zijn o.a. symmetrisch, concentrisch, samengesteld en ultra-magisch.
bronnen
Nederlands
- Magische vierkanten (ing. P.H. Stikker - PDF)