2. Substituteren
Bij 't oplossen van een stelsel van vergelijkingen met de de substitutiemethode druk je een variabele uit in een andere variabele. Je kunt dan die variabele vervangen door die uitdrukking. 'Substitueren' betekent 'vervangen'.Voorbeeld
\begin{array}{l} \left\{ \begin{array}{l} x + y = 2 \\ y = x^2 + 2 \\ \end{array} \right. \\ \left\{ \begin{array}{l} x + x^2 + 2 = 2 \\ y = x^2 + 2 \\ \end{array} \right. \\ \left\{ \begin{array}{l} x^2 + x = 0 \\ y = x^2 + 2 \\ \end{array} \right. \\ \left\{ \begin{array}{l} x(x + 1) = 0 \\ y = x^2 + 2 \\ \end{array} \right. \\ \left\{ \begin{array}{l} x = 0 \\ y = x^2 + 2 \\ \end{array} \right. \vee \left\{ \begin{array}{l} x = - 1 \\ y = x^2 + 2 \\ \end{array} \right. \\ \left\{ \begin{array}{l} x = 0 \\ y = 2 \\ \end{array} \right. \vee \left\{ \begin{array}{l} x = - 1 \\ y = 3 \\ \end{array} \right. \\ \end{array}
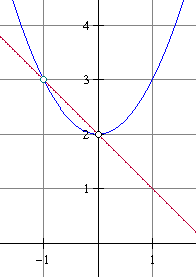
De oplossing: (-1,3) en (0,2)
Vragen en antwoorden
- Vergelijkingen oplossen
- Stelsel van twee vergelijkingen met twee onbekenden oplossen
- Oplossen stelsels vergelijkingen