9. Vergelijkingen met absolute waarde oplossen

 Voorbeeld

Los op: \left| {x - 1} \right| + \left| {x + 1} \right| = 2

Eerst maar 's de grafiek!?

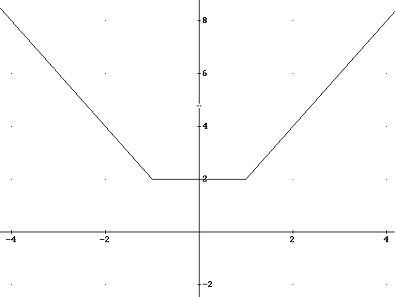
p1572img1.gif

Waarschijnlijk kan je nu de oplossing al wel zien. Maar hoe bereken je dat?

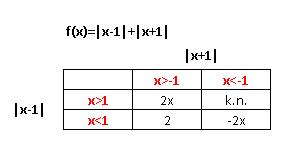
p1572img2.gif

  1. Als x-1>0 en x+1>0 dan gaat het functievoorschrift over in x-1+x+1=2x.
  2. Als x-1>0 en x+1<0 dan zou x>1 en x<-1 moeten zijn, maar dat kan niet.
  3. Als x-1<0 en x+1>0 dan x<1 en x>-1 dan gaat de functie over in -x+1+x+1=2.
  4. Als x-1<0 en x+1<0 dan is x<-1 dan gaat de grafiek over in -x+1+-x-1=-2x.

De vergelijking \left| {x - 1} \right| + \left| {x + 1} \right| = 2 heeft als oplossing -1\leqx\leq1

F.A.Q.

Terug Home