\require{AMSmath}

Voorbeeld 1

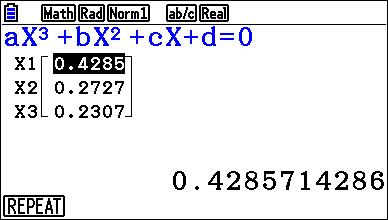
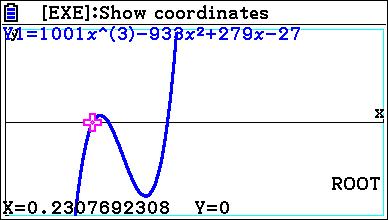
Je wilt de vergelijking 1001x^3-933x^2+279x-27=0 oplossen.

De waarde van d is niet nul dus je kunt geen x buiten haakjes halen. Er is ook niet direct een voordehandliggende oplossing in beeld. Je GR geeft mogelijk ook niet direct uitsluitsel.

De formule van Cardano

Invullen van de coëfficiënten a t/m d in de formule van Cardano geeft:

\eqalign{   & p =  - \frac{{10884}} {{1002001}}  \cr   & q =  - \frac{{358720}} {{1003003001}}  \cr   & W = \frac{{144i\sqrt 3 }} {{1002001}}  \cr   & x = \frac{3} {7} \cr}

Je kunt dan verder oplossen met ontbinden. Eerst maar 's de staartdeling:

\eqalign{ & x - \frac{3} {7}/1001x^3 - 933x^2 + 279x - 27\backslash 1001x^2 - 504x + 63 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline {1001x^3 - 429x^2 } \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - 504x^2 + 279x - 27 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline { - 504x^2 + 216x} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,63x - 27 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline {63x - 27} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0 \cr}

Dat schiet al lekker op...

Je krijgt:

\eqalign{ & 1001x^3 - 933x^2 + 279x - 27 = 0 \cr & \left( {x - \frac{3} {7}} \right)\left( {1001x^2 - 504x + 63} \right) = 0 \cr & x = \frac{3} {7} \vee 1001x^2 - 504x + 63 = 0 \cr & ... \cr}

Met de ABC-fomule:

\eqalign{ & x_{2,3} = \frac{{504 \pm \sqrt {\left( { - 504} \right)^2 - 4 \cdot 1001 \cdot 63} }} {{2 \cdot 1001}} = \frac{{504 \pm \sqrt {1764} }} {{2002}} \cr & x_2 = \frac{{504 - \sqrt {1764} }} {{2002}} = \frac{3} {{13}} \cr & x_3 = \frac{{504 + \sqrt {1764} }} {{2002}} = \frac{3} {{11}} \cr}

Oplossing

\eqalign{ & 1001x^3 - 933x^2 + 279x - 27 = 0 \cr & \left( {x - \frac{3} {7}} \right)\left( {1001x^2 - 504x + 63} \right) = 0 \cr & x = \frac{3} {7} \vee 1001x^2 - 504x + 63 = 0 \cr & x = \frac{3} {7} \vee x = \frac{3} {{11}} \vee x = \frac{3} {{13}} \cr}

Opgelost...

©2004-2025 WisFaq