Je wilt de vergelijking
x^3 - 5x^2 - 12x - 96 = 0
oplossen. De waarde van d in ongelijk aan nul en er is niet direct een eenvoudige oplossing zichtbaar.
Je kunt voor het oplossen van de vergelijking ook de grafische rekenmachine gebruiken. Afhankelijk van het merk en type zijn er verschillende mogelijkheden.
CASIO fx-CG50
Op een CASIO fx-CG50 gaat dat zo:
Kies uit het menu de optie Equation:

Kies voor Polynomial:

Kies voor Degree=3:

Vul de waarden voor a t/m d in:

...en kies voor SOLVE:
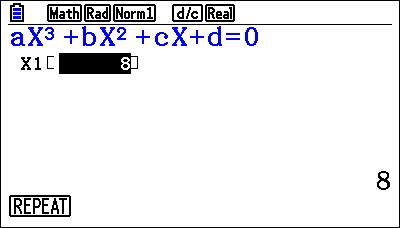
Dat geeft je de oplossingen... of in dit geval één oplossing.
Dat laatste had je misschien niet verwacht, maar een derdegraadsvergelijking kan 1, 2 of 3 oplossingen hebben. Hieronder heb ik de grafiek getekend. Dan zie je hoe dat zit.
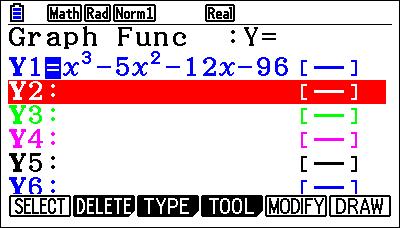
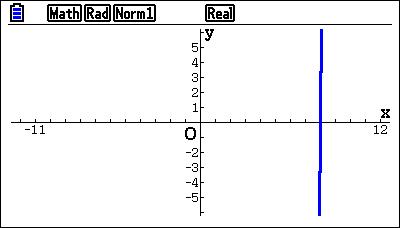
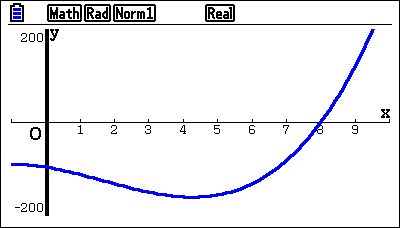
Opgelost...
NASCHRIFT
Nu je weet dat x=8 een oplossing is zou je de vergelijking ook kunnen oplossen m.b.v. van ontbinden met x-1. Gebruik daarbij een staartdeling. Uiteindelijk krijg je:
\begin{array}{l} x^3 - 5x^2 - 12x - 96 = 0 \\ (x - 8)(x^2 + 3x + 12) = 0 \\ x - 8 = 0 \vee x^2 + 3x + 12 = 0\,\,(v.n.) \\ x = 8 \\ \end{array}
...en dat is dan dat...

