Ik heb 100 getallen varierend van 3,4 tot 8,5. Uiteraard kan je van zo'n rijtje getallen het gemiddelde uitrekenen (afhankelijk van het meetnivo!) en andere centrum- of spreidingsmaten. Maar echt overzichtelijk is het niet.
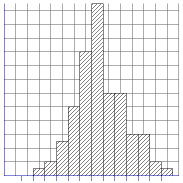
Daarom verdelen we de getallen in klassen. Laten we maar eens als eerste klasse [3;3,5> nemen. Je krijgt dan fig.1. Dit geeft al een aardig beeld van de verdeling.
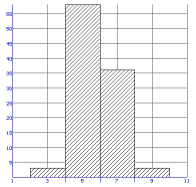
Nemen we [3,5> als eerste klasse, dan krijgen we het fig.2 Nu zijn we wel erg veel informatie kwijt geraakt. Met maar 4 staven kan je niet veel meer.
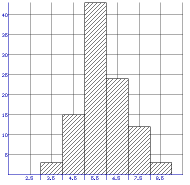
Laten we [3,4> als eerste klasse nemen (fig.3). Dit lijkt ook een redelijke klassenindeling. Het plaatje geeft in ieder geval een mooi overzicht van de verdeling. Maar het hangt natuurlijk af van de situatie en hoe 'precies' de verdere berekeningen moeten zijn.
Uiteraard raak je op deze manier informatie kwijt. Bij het berekenen van centrum- en spreidingmaten ga je er bijvoorbeeld steeds van uit dat het gemiddelde in zo'n klasse het klassemidden is.
Notaties
In schoolboeken worden de volgende notaties voor klassen gebruikt:
-
12-20: betekent 12 tot en met 20
Het hangt dan af van de situatie wat precies de verdeling is. Bijvoorbeeld bij 'gewicht in kilogram' betekent 12-20 in intervalnotatie [11,5;20,5>. Bij leeftijd zou 12-20 in intervalnotatie [12,21> zijn.
-
12-<20: betekent 12 tot 20
Dit kan verwarrend zijn. Neem aan dat het over gewicht gaat... wat betekent dan 12-<20? Als het goed is betekent het [12,20>, toch?
Persoonlijk geef ik de voorkeur aan de 'normale' intervalnotatie. [12,20> is voor iedereen duidelijk. De klassebreedte is 8, de linker klassegrens is 12 en de rechter klassegrens is 20. Weinig aanleiding tot verwarring!
F.A.Q.

