Loading jsMath...
\require{AMSmath}

Voorbeeld

Domein van f(x) = \sqrt {x^2  - 1}

 <  \leftarrow , - 1] \cup [1, \to  >

Nulpunten zijn (-1,0) en (1,0). De functie is overal groter of gelijk aan nul.

 p1909img1.gif

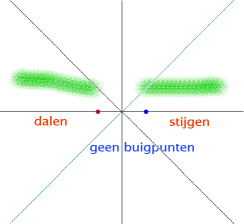
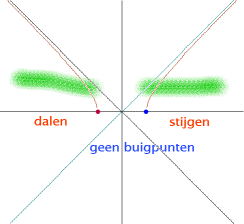
Stijgen en dalen:

f'(x) = \large{x \over {\sqrt {x^2  - 1} }}

 

 p1909img3.gif

Geen maxima en minima

 p1909img4.gif

Geen buigpunten

 p1909img5.gif

Asymptoten:

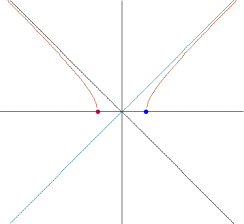
y=-x en y=x

 p1909img6.gif
Grafiek tekenen p1909img7.gif


©2004-2025 WisFaq