Matrixvermenigvuldiging
Bij het vermenigvuldigen van matrices zijn twee zaken van belang:- Kloppen de afmetingen van de twee matrices ?
- Heeft de vermenigvuldiging betekenis ?
1. Kloppen de afmetingen van de matrices ?
Twee matrices vermenigvuldig je door steeds een rij van de eerste matrix met een kolom van de tweede matrix te vermenigvuldigen.
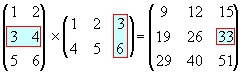
Daaruit volgt dat om twee matrices te kunnen vermenigvuldigen het aantal kolommen van de eerste matrix gelijk moet zijn aan het aantal rijen van de tweede matrix.
Het resultaat van een vermenigvuldiging van een 3x2 matrix met een 2x3 matrix is een 3x3 matrix. Om dat te onthouden kun je denken aan:
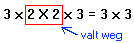
Het getal in de productmatrix dat op de tweede rij in de derde kolom staat is dus het product van de tweede rij van de eerste matrix en de derde kolom van de tweede matrix.
2. Heeft de vermenigvuldiging betekenis ?
Deze vraag is moeilijker te beantwoorden. De beste manier is om één van de getallen uit de productmatrix na te rekenen en dan precies na te gaan wat je nu eigenlijk doet.Voorbeeld
Je kunt een directe-wegen matrix met zichzelf vermenigvuldigen. De productmatrix noemen men wel het kwadraat van de matrix.
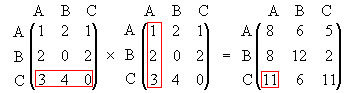
Waar komt die 11 in de derde rij, eerste kolom vandaan ?
Je vermenigvuldigt de derde rij met de eerste kolom dus:
3 · 1 + 4 · 2 + 0 · 3 = 11
Maar wat is de betekenis ?
Je kunt op 3 manieren van C naar A.
Je kunt op 1 manier van A naar A.
Dus 3 · 1 levert het aantal manieren om in 2 stappen van C naar A te gaan (via A).
Je kunt op 4 manieren van C naar B.
Je kunt op 2 manieren van B naar A.
Dus er zijn 8 manieren om in 2 stappen van C naar A te gaan (via B).
Je kunt niet (direct) van C naar C.
Dus ook niet in 2 stappen van C naar A (via C).
Als je deze 3 en 8 (en 0) optelt krijg je 11. Het aantal manieren om in 2 stappen van C naar A te gaan is 11.
In de productmatrix kun je het aantal tweestapswegen aflezen.
Nog een aanwijzing..
In NETWERK 4 havo A staat op blz.234 een mooie opgave:
|
Een beleggingsfonds belegt in onroerend goed, aandelen en obligaties. Het fonds doet de beleggingen in Duitsland, Japan, de VS en Nederland. Hieronder staat een overzicht van de beleggingen, uitgedrukt in de munteenheid van de betreffende landen. Alle getallen moeten met 1 miljoen vermenigvuldigd worden.
Het fonds wil de aandeelhouder een overzicht presenteren van de beleggingen. Omdat de meeste aandeelhouders in Nederland wonen, maakt het fonds een overzicht in guldens. Daarnaast maakt ze voor haar buitenlandse aandeelhouders een overzicht in dollars. Bij de berekeningen gaat het fonds uit van de volgende koersen.
In de tabel kun je bijvoorbeeld aflezen dat 1 dollar f 2,09 waard is.
|
Om te beginnen kiezen we:
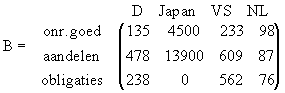
Hoe ziet nu K eruit ?
Op grond van het bovenstaande weten we in ieder geval dat K een matrix moet worden met 4 rijen. Omdat we de beleggingen zowel in gulden als in dollars willen uitrekenen zal deze matrix 2 kolommen moeten hebben.
Stel je voor we nemen:
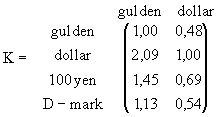
De afmetingen kloppen, maar B · K slaat helemaal nergens op:
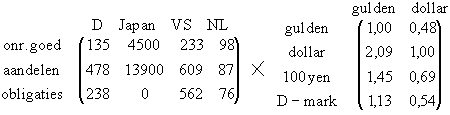
Ga maar na, als je de eerste rij keer de eerste kolom uit zou rekenen, vermenigvuldig je 135 miljoen D-mark in onroerend goed met de koers van de Nederlandse gulden in gulden.
Kortom de randen van de matrices kloppen NIET.
De volgende matrix is beter:
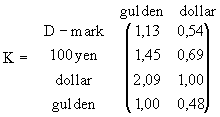
Je krijgt dan de volgende vermenigvuldiging:
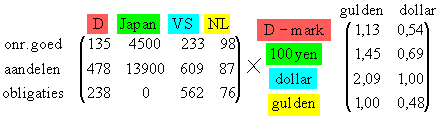
Dat ziet er goed uit, maar er zit toch nog een foutje in. Dat foutje mag je proberen zelf te bedenken!
F.A.Q.
- Rekenen met matrices: vermenigvuldiging
- Matrixvermenigvuldiging
- Waar zit de muis?
- Overgangsmatrices 1
- Overgangsmatrices 2
- Overgangsmatrices 3
- Een vitaminetekort